In 1909, German physicist Paul Ehrenfest proposed a paradoxical situation arising from the newly-minted Special Theory of Relativity. If a cylinder (or disk) were rotated about its axis such that the surface travelled at a relativistic speed, the circumference should experience Lorentz-Fitzgerald contraction. The radius, moving sideways, would not contract, therefore the ratio between the two would change, altering the value of pi (π).
This century-old paradox has generated a mountain of papers proving and disproving the proposition that a circle can change its circumference without changing its diameter. Common sense would say that measuring the circumference of a disk rotating on a fixed platform would be done with measuring rods mounted on the fixed platform, not subject to any contraction, and would remain the same regardless of how fast the disk were rotating. Nevertheless, much math has been offered to prove otherwise.
Pi is heavily woven into the fabric of the universe, and changing it is a cause for concern. Having an untethered value of pi is especially upsetting because it sits as a constant in General Relativity's "Einstein Equation":
Gμν=8πGTμν/c4 ,
which runs much of the universe. A fundamental constant varying with states of rotation is not good in a universe where most everything is in some state of rotation.
Shooting down the paradox is therefore a desirable goal, yet a majority of Ehrenfest papers deliver massive amounts of math in support of it.
Special Relativity is special in that it applies only in inertial reference frames. Einstein saw that an accelerating frame like gravity gummed up the works, so he moved on to figure out General Relativity, leaving the rest of us to work on Ehrenfest's stumper. A rotating frame is an accelerating frame, so application of the SR transforms cannot be automatically assumed.
Special Relativity has four main effects. Time dilation and mass increase do apply in rotation, demonstrated in circular cyclotron particle accelerators. The other two effects, Lorentz contraction and Relativity of Simultaneity (RoS) do not lend themselves to experimental verification, but come out of the math required to maintain a constant speed of light.
The paradox relies on the application of Lorentz contraction to the rotating reference frame, but its sister effect of RoS is often ignored in papers. This is unfortunate, for the two go together - you don't get one without the other.
Relativity of Simultaneity is the case where observers in different reference frames do not agree on whether two events occurred at the same time. Einstein gave an example of this, using the fastest thing moving in 1905, a railroad train. The top locomotives could go well past a hundred miles per hour on a straight stretch, while the Wright brothers were only hitting the low double digits.
We place an observer at a train station, and another midpoint on an express train travelling at high speed past the station, able to see synchronized clocks at the locomotive and caboose.
At the instant the train observer is abeam the station observer, a lightning bolt comes down, splits in two, and strikes the locomotive and caboose at the same time in the station frame. The station observer sees the flashes at the same time, and as they appear the same distance from him, he judges them simultaneous.
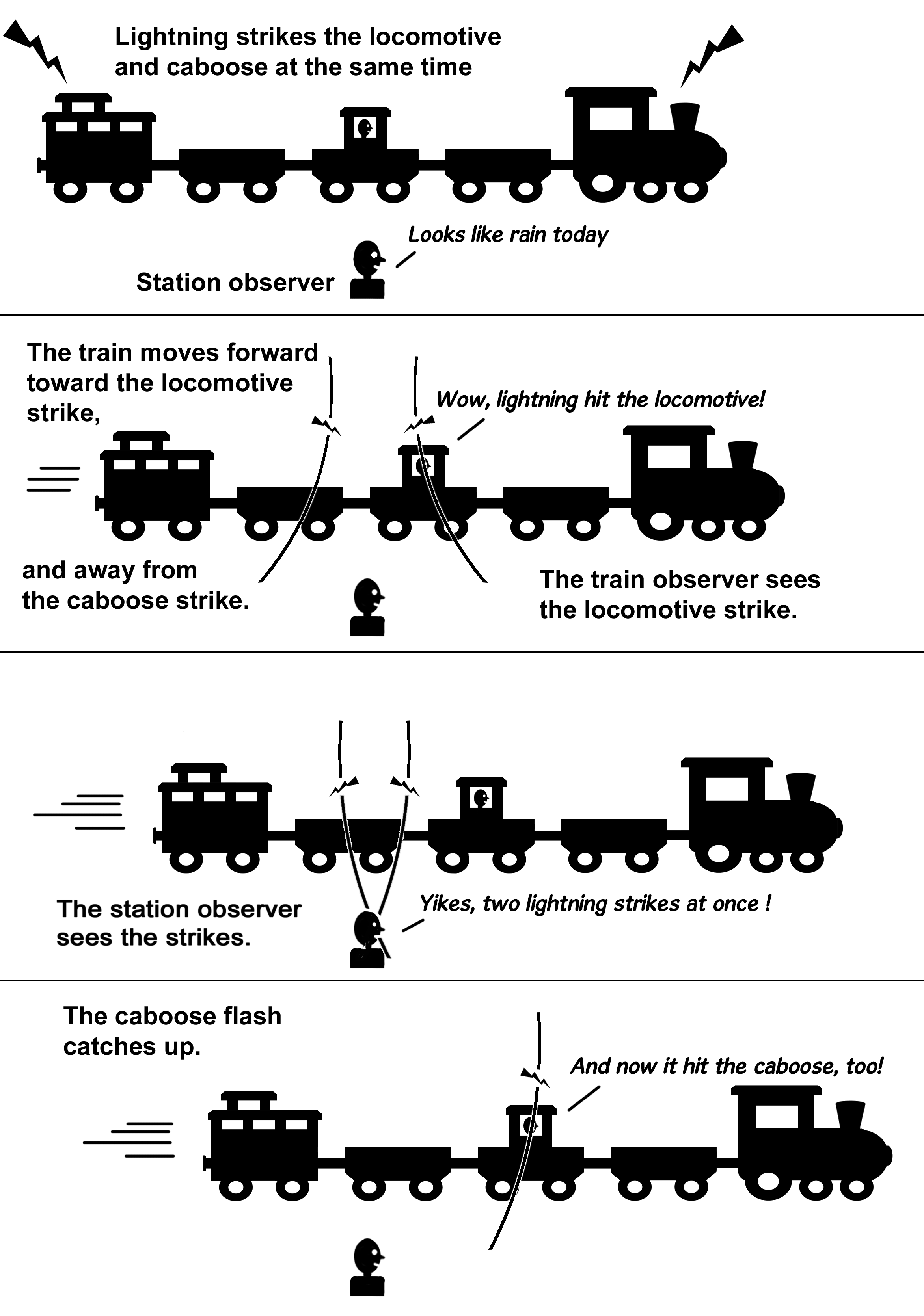
The light flashes move toward the center of the train, but in their brief travel time, the train and the central observer have moved forward in the direction of the locomotive flash, and away from the caboose flash. The train observer thus sees the locomotive flash first, and then the caboose flash catches up with him. They appear the same distance away, so he judges them not simultaneous. A straightforward example of RoS from Einstein.
There is another effect of RoS though. The conductor has set all the clocks on the train, and the train observer can see them from his mid-position. Here is a definitely-not-to-scale time sequence of the two lightning events for the train observer:
1157
1158
1159 - lightning flash illuminates the locomotive clock.
1200
1201 - lightning flash illuminates the caboose clock.
1202
As expected, the locomotive flash shows an earlier time than the caboose flash.
Here then is the other RoS effect:
The station observer can also see the clocks. He sees the flashes at the same time, but he sees the clocks on the train unsynchronised, one reading 1159 and the other reading 1201. RoS produces a time shift, where leading clocks read earlier than trailing clocks.
Now let's look at length. We'll define length as the distance measured between two ends of an object.
We have 10 inch Central American caterpillar moving along at two inches per second. We mark the position of the tail on the ground, then two seconds later mark the position of the head. 14 inches. Try again. We mark the head first, then two seconds later mark the tail. 6 inches. We need to add a caveat to our definition: "measured at the same time." We now get 10 inches.
This is how Lorentz contraction occurs. Two reference frames moving relative to each other have different ideas of "at the same time." With Lorentz contraction, the time shift on the object moving through our frame produces the 6 inch caterpillar.
Let's run our train on a circular track. The paradox requires Lorentz contraction, so we assume we have it, and necessarily its sister, Relativity of Simultaneity. Running the train around, we don't learn much other than it's shorter and the locomotive clock reads earlier than the caboose clock.
So we stretch things out by adding cars to the train, so many that the train covers the track completely, running the locomotive right up against the caboose. RoS says that as the conductor moves forward from the caboose to the locomotive, setting clocks along the way, we station observers see the time getting earlier and earlier. When the conductor gets to the locomotive, his clock is reading earlier than the clock in the caboose just in front of him. Puzzled, he heads back around the circle to the caboose, noticing all the clocks he passes are still in sync with his, until he reaches the caboose, and the locomotive nudged up behind him is reading early. A time discontinuity. If he starts clock setting at a different car and completes the circle, the discontinuity occurs wherever he started. Is this an observational quirk, something like quantum oddness, or something else?
It's an indication that our initial assumption was wrong. We can't have Lorentz contraction and RoS on this circular train track, because the time discontinuity produces an impossible situation:
A person at the discontinuity could know the future and change the past.
That isn't allowed in this universe. (Climate scientists and totalitarian governments, respectively, excepted.)
The conductor is resigned to living with the locomotive nudging his caboose. He decides to hold a lottery drawing at 1200. People along the train pick their numbers and time-stamp them, handing the picks to porters to carry back to the caboose.
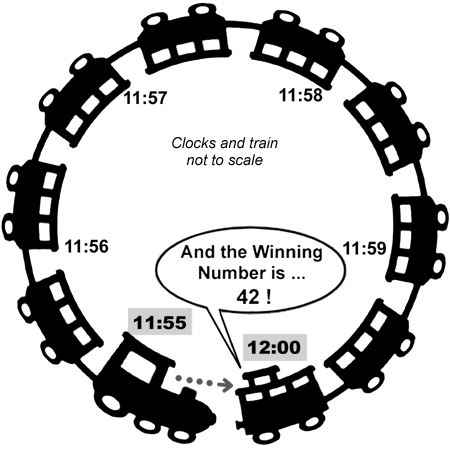
At 1200, the conductor pulls winning #42 out of his hat. The engineer across the discontinuity sees #42, writes it down, and time stamps it at 1155. At 1158, that ticket is somewhere mid-train enroute. It eventually arrives at the caboose, winning the lottery. Knowing the future with certainty.
How about changing the past? The conductor draws #42, but sees the engineer marking his ticket and about to time stamp it at 1155. The conductor pulls out his shootin' iron and plugs that cheatin' engineer first, so the ticket never gets sent. But at 1158, that unsent ticket was somewhere enroute to the caboose, before the conductor shot the engineer at 1200. Or is it? Does it vanish, or arrive? What about the porter?
Ehrenfest produces an impossible situation, not allowed. We cannot have Lorentz contraction and Relativity of Simultaneity in the rotating frame. QED.
We're not done yet. If we don't have Relative Simultaneity, what do we have? Absolute simultaneity?
Yes.
At least with a rotating frame, anyway. Two observers in different states of motion can agree on the simultaneity of two events.
We're done with trains. We take a large disk, with a radius of one light-second. The moon is one and a quarter light-seconds away, so this disk fits easily within the imagination. The disk sits on a non-rotating platform, and has radial lines painted on it every 10 degrees. Out at the rim, we place poles and strobe lights at each line, with matched poles and strobes on the platform, placarded from North (0/360°) clockwise around the rim. We'll rotate the disk counter-clockwise at 10 degrees per second.
As we stand in the center and look out to the rim, we're looking back in time one second, just as we see the moon as it was one and a quarter seconds ago, and Andromeda galaxy two and a half million years ago.
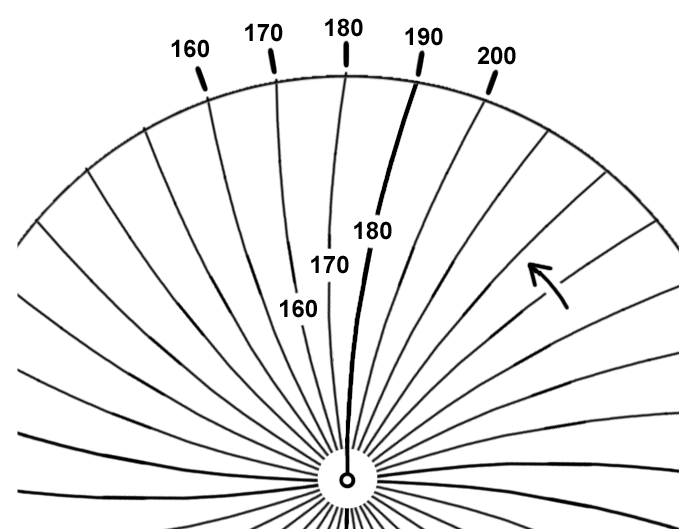
With the disk in slow rotation, we have no trouble staying faced to the South, 180° fixed marker. Our clock is synched with the platform clocks, so we know when the disk markers are aligned with their platform twins, once every 36 seconds. When we look south at an alignment time, we don't see the 180° line hitting the 180° platform marker, but the 190° marker instead, which it actually hit one second ago. The 180° line starts south, but then curves gently to the right to hit the 190° marker, where it was one second earlier. All the lines do this, curving right to where they were a second ago. We understand this time delay, so no problem.
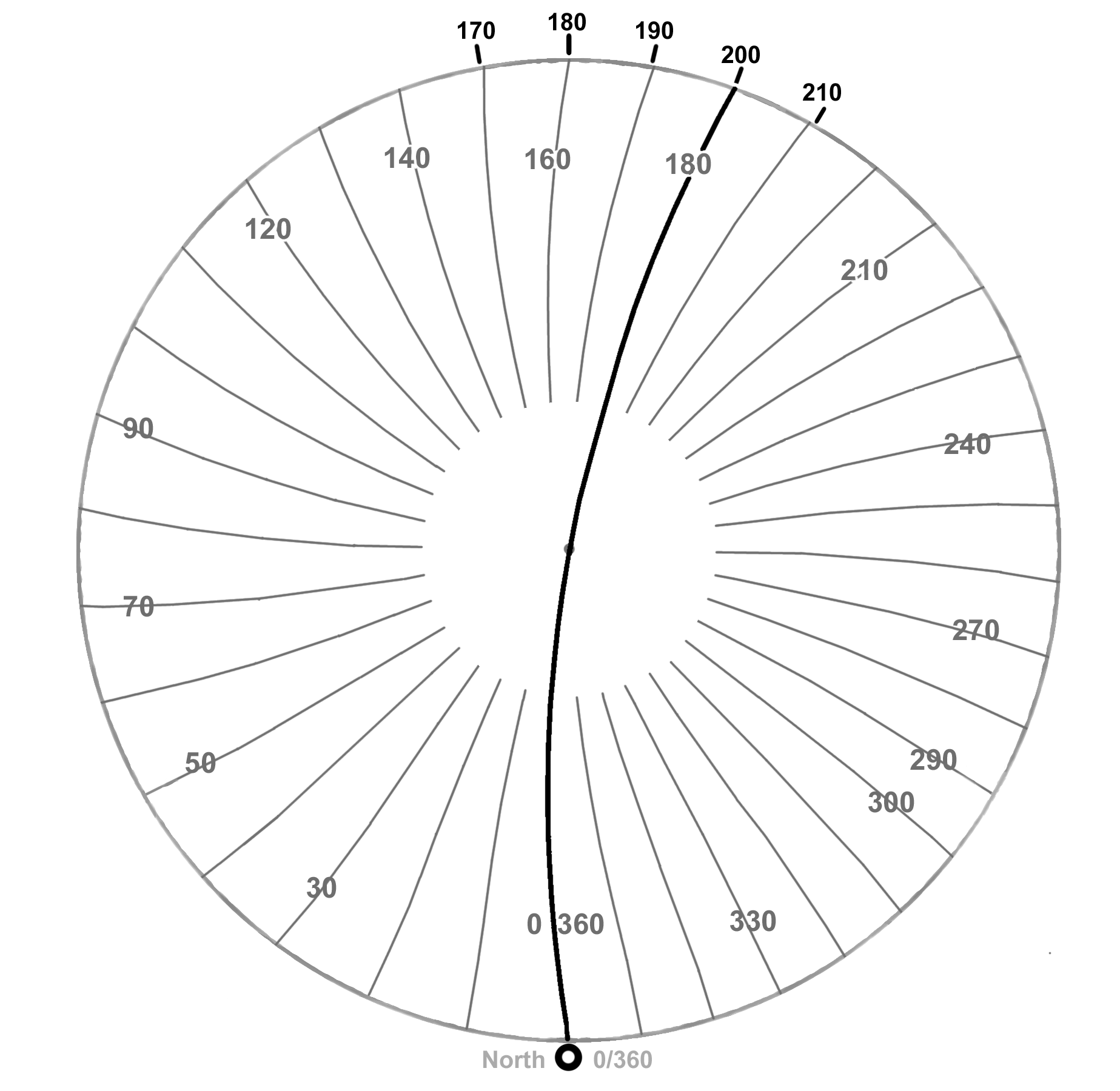
Let's move from the center to the North 0/360° marker, and step off the disk. Now as we look two light-seconds across to the 180° platform marker, it's the 160° line hitting it. The 0/360°-180° diameter line bows slightly away to the left, returns to the center at the center, then curves gently off 20 degrees right this time. Again, we understand how the time delay distorts the rotating disk.
But look at what we have visually. We're seeing a circular disk, with 160 stretched degrees on its left half, and 200 degrees squeezed into the right half. We know what's going on, but it still looks strange.
We see this configuration once a second, every time a radial line passes us, but an observer on the rim and moving with the disk will see this continuously.
No lightning, but strobe lights this time. Strobes at the platform 60° and 300° markers will flash at the next great alignment. One second later we'll see the flashes. They appear the same distance away, seen at the same time, we judge them simultaneous.
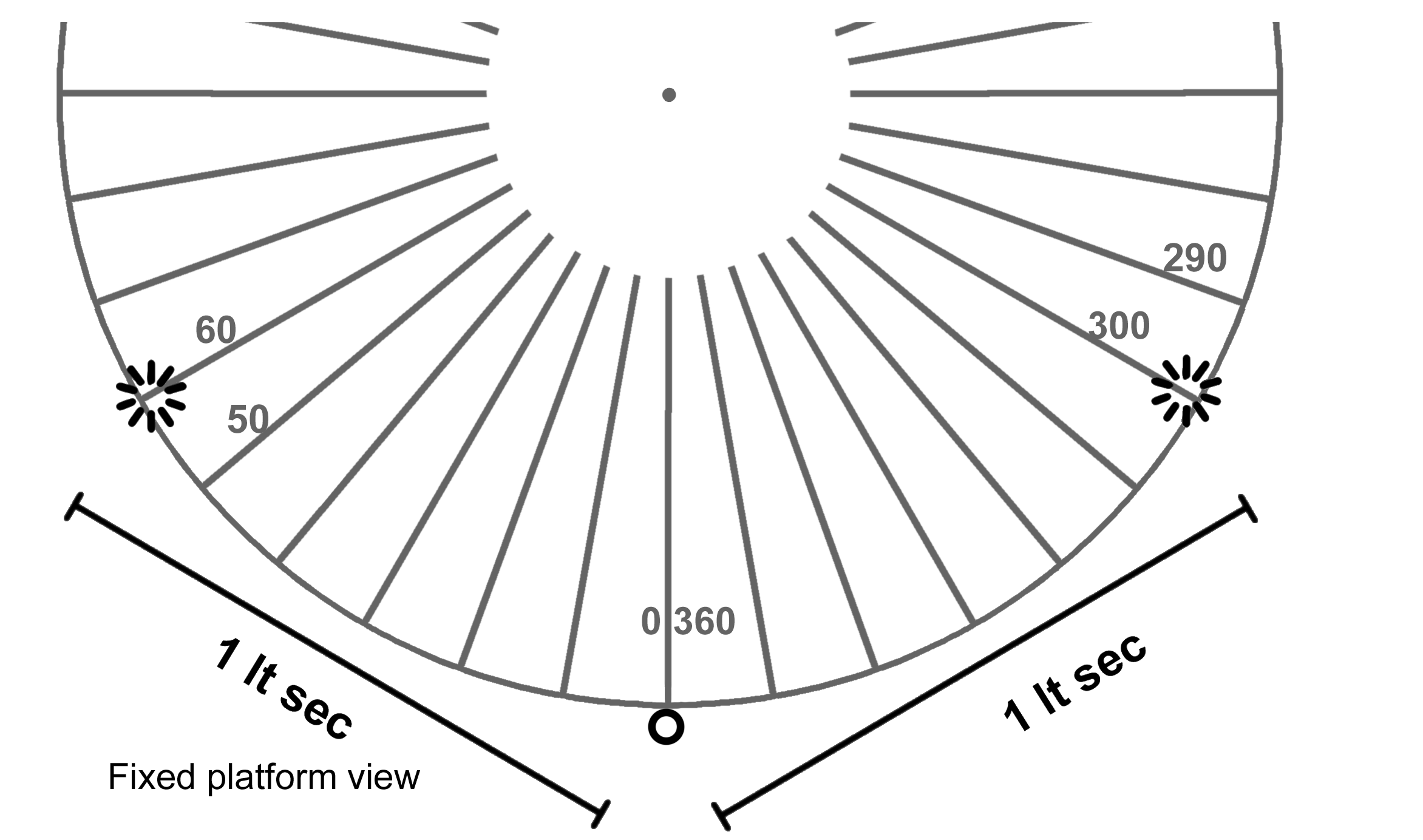
A rim-riding observer however, passing the North marker when the strobes fire will rotate on to the right, towards the 300° marker and away from the 60° marker. Like the train observer, he'll see the approaching flash first and the receding flash second. But here's the difference - the 300° marker is squeezed closer to him, and 60° marker is stretched away from him, so he naturally expected the 60° strobe to flash later. A little pencil and paper calculation will tell him that yes, they were simultaneous, in agreement with us fixed observers.
Now we change the strobes around so that the rim-rider will see them at the same time. We place one strobe near the 50° marker, and move the other near the 290° marker.
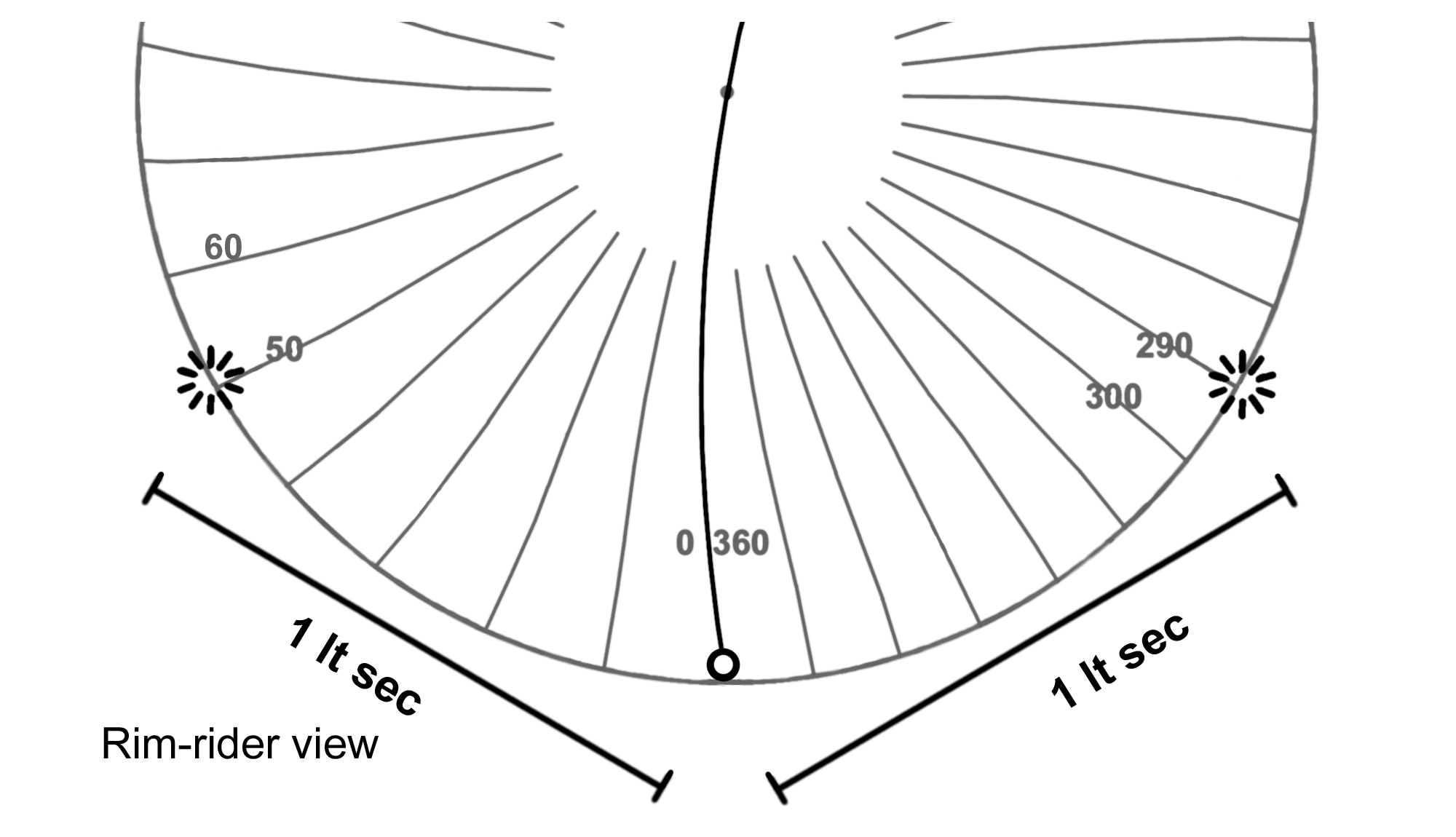
The rim-rider passes us at North alignment and the strobes fire. We of course see the 50° strobe first, since it appears closer to us, and then the more distant 290° strobe. Pencil and paper again tells us yes, simultaneous. The rim-rider sees them at the same time, and they appear in his twisted world to be the same one light-second (before any time dilation adjustment) away from himself, so he, too, judges them simultaneous.
Observers in two very different reference frames, one inertial and one rotating and accelerating, agree on simultaneity. Absolute simultaneity.
One thing to be thankful for is that the Creator trashed the Luminiferous Ether model and went for General Relativity instead. The world would be a strange place otherwise —
We are on a planet that rotates once a day, about 700 mph at mid-latitude, orbits the sun at 18 plus miles per second, and cruises through the galaxy at roughly 140 miles per second toward Sagittarius. Like on the disk, we would see things in the direction we were going squeezed together, and stretched out in the direction we came from. And this direction would rotate around us once every day.
And gravity wouldn't work right.
____________________________________________
Notes:
The rim-rider will have negligible time dilation - 0.985 normal rate, but even substantial dilation would not impair his ability to tell if two events are simultaneous.
He will also experience stellar aberration, a small shifting of items in his visual field in the direction of his motion. This also will not affect his ability to determine simultaneity.
Relativity of Simultaneity is not strictly a relativistic effect. It also affects the thunderclaps from the train lightning strikes. The station observer will hear the two strikes at the same time, while the train observer will hear the locomotive strike first, just as he sees the locomotive strike first.